Noise Modifications for 'Breaking a 5-Bit Elliptic Curve Key'
All Backend Data ZIP Download
These experiments are noise-control tests for my arXiv paper 'Breaking a 5-Bit Elliptic Curve Key using a 133-Qubit Quantum Computer'.
arXiv Link
1. No-QFT Pure Hardware Noise (Baseline Run)
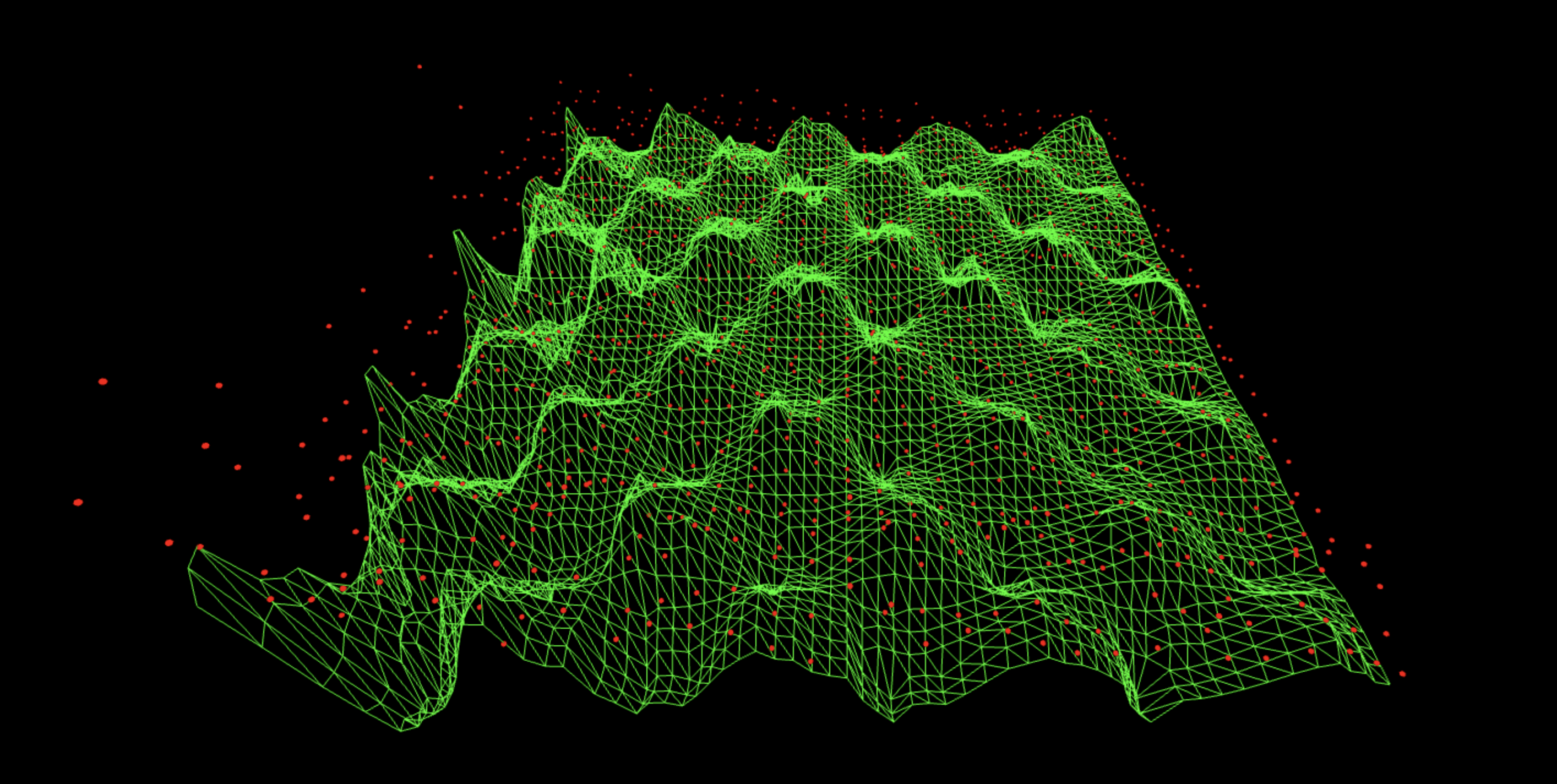
Removing both QFTs and measuring the unordered a- and b-superposition produces uniform noise. No lanes, no valleys, no ridges. This shows the backend’s small local fluctuations from decoherence and readout drift. The absence of any geometry here shows how important the QFTs and the oracle-generated phase relation is for producing the interference lanes in the real 5-bit Shor-style run.
 Calibration SS.png)
 Calibration Back SS.png)
 image.png)
2. Dual QFTs, No Structure (Fully Scrambled Registers)
When both a and b are placed into full superposition, phase-scrambled, and then run through two clean QFTs with no structure, the output no longer forms a ridge, just shallow, noisy oscillations. You can see unevenly spaced vertical and horizontal ripples. Without the aP + bQ phase oracle, the Fourier map has nothing to lock onto, so the landscape flattens into weak wave texture and noise.
 SS.png)
 Back SS.png)
 Image.png)
3. Randomized QFTs With Inverted Fourier Partition
Splitting a ∪ b into two random QFT groups destroys regular frequency reinforcement. Instead of interference bands the output collapses into a low noise floor with a handful of uneven spikes clustered off to one side and faint periodic vertical points. This run shows that once the Fourier space is partitioned improperly, the quantum computer has no route to build interference, randomness stays random, only reshuffled into scattered amplitude peaks.
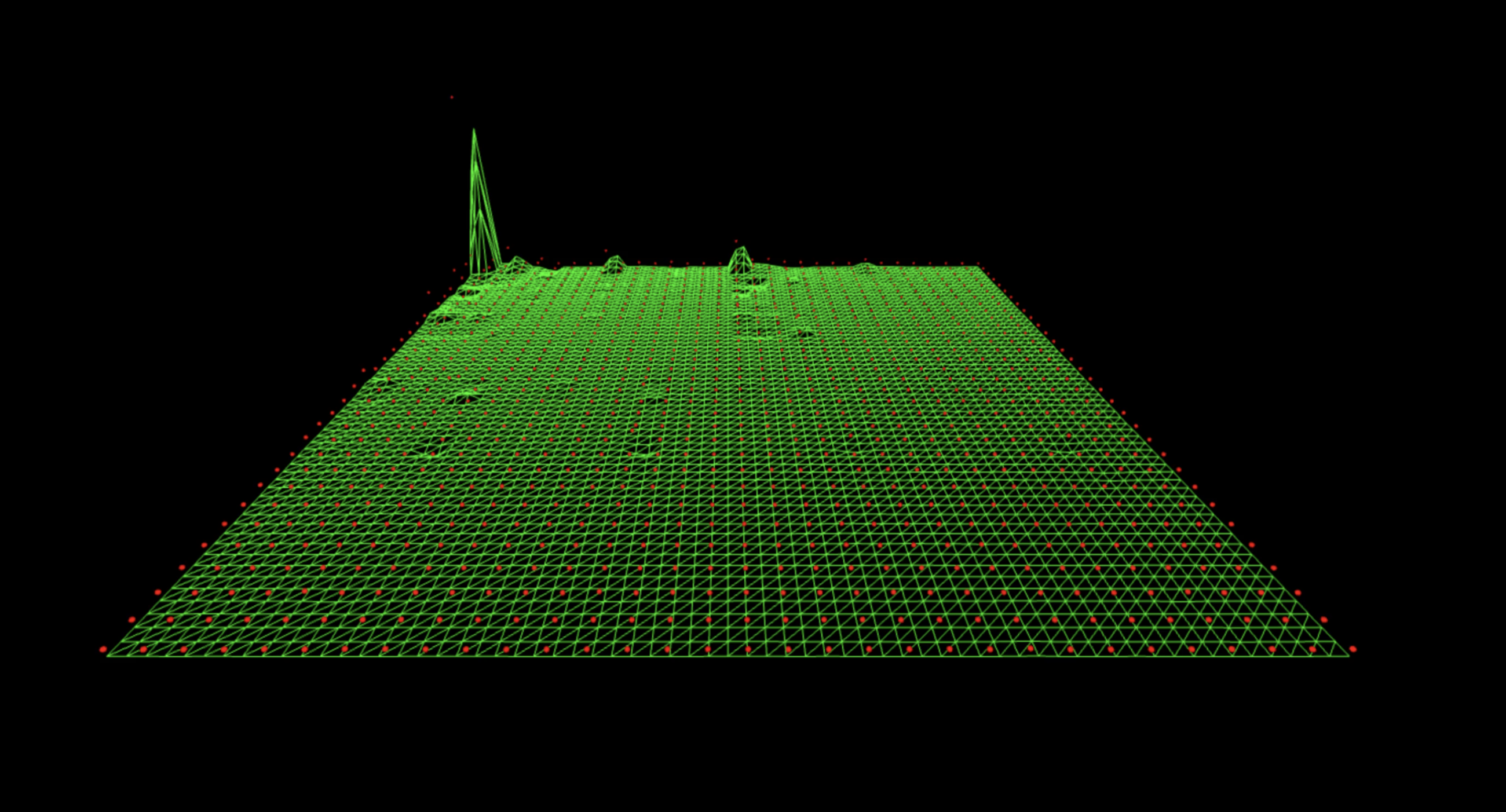
4. Single QFT, No Structure (Fully Scrambled Registers)
Both a and b are placed into full superposition, phase-shifted with fixed per-qubit RZ masks, and then passed through one global QFT with no oracle structure. The result shows faint periodic ripple-bands across the surface, on the left they sharpen into turbulent high-frequency spikes, while the right half collapses into smoother low-frequency modes with probability concentrating into only a few bins, strongest in the upper-right and lower-right corners.
 SS.png)
 Back SS.png)
 Image.png)
5. Random Partition QFT (One transform only, no oracle)
With all 10 qubits in superposition but randomly split before a single QFT is applied, the Fourier space fractures instead of unifying, producing an asymmetric landscape, one half collapses into a flat, near-thermal sheet while the mixed region forms scattered interference spikes where subspaces briefly align. No global ridges appear, only local vertical bursts, showing what happens when the QFT doesn’t span the full Hilbert space.
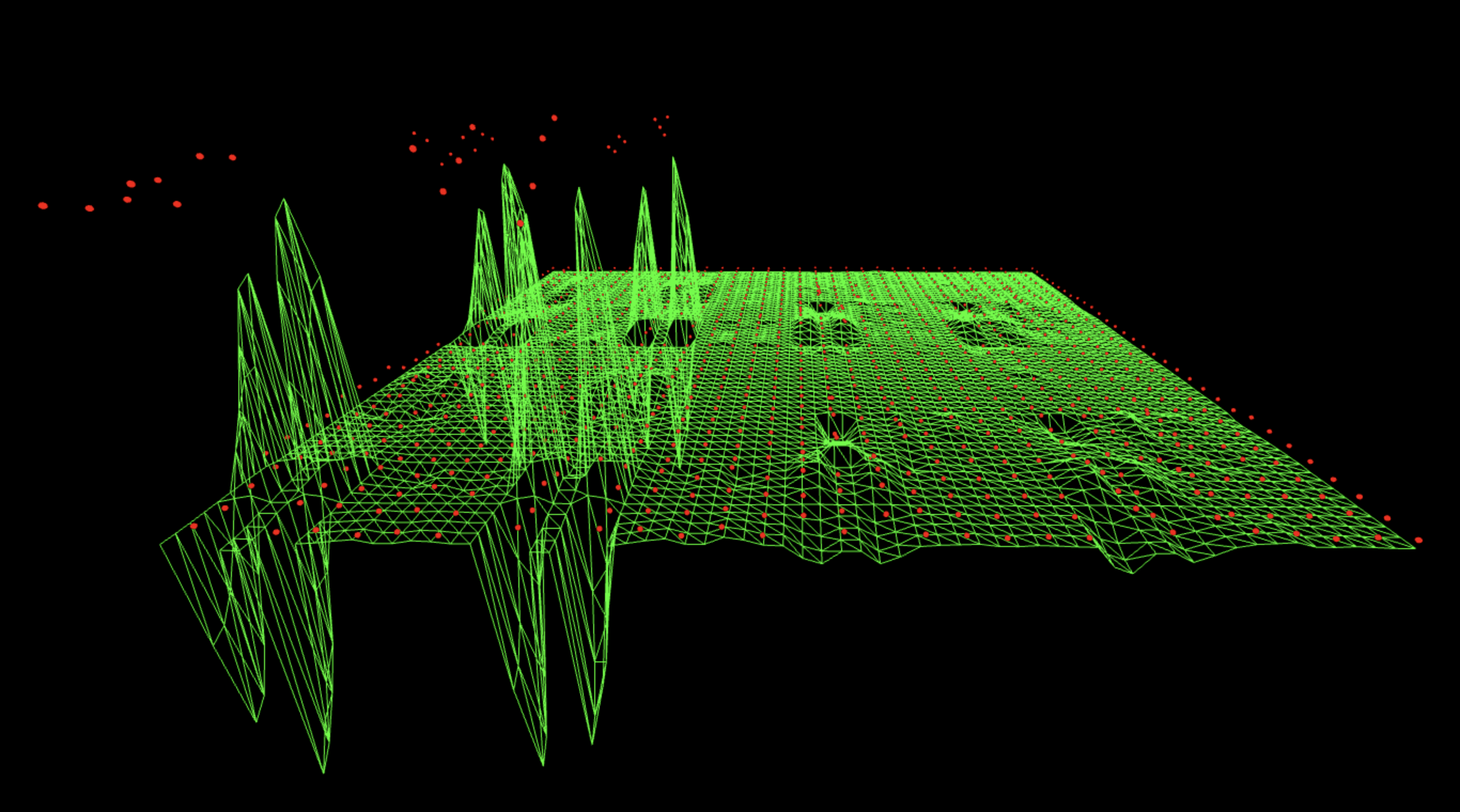
6. Real Oracle and single 10-Qubit QFT
This run uses the full oracle exactly as in the 5-bit arXiv paper, but replaces the two separate 5-qubit QFTs with a single 10-qubit QFT across a ∪ b. The four vertical interference lanes vanish completely and are replaced by one broad, chaotic ridge with no vertical periodicity and no discernible subgroup structure. Even with perfect aP + bQ phases, the joint Fourier basis destroys the geometry that creates the interference lanes, ridges, and valleys.
Code:
# No-QFT Pure Hardware Noise (Baseline Run)
# Imports
import logging, json
from math import gcd
import numpy as np
from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister, transpile
from qiskit.circuit.library import UnitaryGate
from qiskit_ibm_runtime import QiskitRuntimeService, SamplerV2
import pandas as pd
# IBMQ
TOKEN = ""
INSTANCE = ""
BACKEND = "ibm_fez"
CAL_CSV = "/Users/steventippeconnic/Downloads/ibm_fez_calibrations_2025-11-22T03_35_21Z.csv"
SHOTS = 16384
# Group parameter (so gcd / inverse logic is identical)
ORDER = 32 # |E(F_p)| = 32
# Logging
logging.basicConfig(level=logging.INFO,
format="%(asctime)s | %(levelname)s | %(message)s")
log = logging.getLogger(__name__)
# Calibration-based qubit pick
def best_qubits(csv_path: str, n: int) -> list[int]:
df = pd.read_csv(csv_path)
df.columns = df.columns.str.strip()
winners = (
df.sort_values(["√x (sx) error", "T1 (us)", "T2 (us)"],
ascending=[True, False, False])
["Qubit"].head(n).tolist()
)
log.info("Best physical qubits: %s", winners)
return winners
N_Q = 5
N_Q_TOTAL = N_Q * 3 # a, b, point
PHYSICAL = best_qubits(CAL_CSV, N_Q_TOTAL)
# Constant-adder modulo 32 as a reusable gate (unused in noise run, kept for structure)
def add_const_mod32_gate(c: int) -> UnitaryGate:
"""Return a 5-qubit gate that maps |x⟩ ↦ |x+c (mod 32)⟩."""
mat = np.zeros((32, 32))
for x in range(32):
mat[(x + c) % 32, x] = 1
return UnitaryGate(mat, label=f"+{c}")
ADDERS = {c: add_const_mod32_gate(c) for c in range(1, 32)}
def controlled_add(qc: QuantumCircuit, ctrl_qubit, point_reg, constant):
"""Apply |x⟩ → |x+constant (mod 32)⟩ controlled by one qubit."""
qc.append(ADDERS[constant].control(), [ctrl_qubit, *point_reg])
# Noise oracle same call site, but no operation
def ecdlp_oracle(qc, a_reg, b_reg, point_reg):
# No-op oracle for pure hardware noise.
return
# Build the full noise circuit with NO QFT (pure hardware noise baseline)
def shor_ecdlp_noise_noqft_circuit() -> QuantumCircuit:
a = QuantumRegister(N_Q, "a")
b = QuantumRegister(N_Q, "b")
p = QuantumRegister(N_Q, "p")
c = ClassicalRegister(N_Q * 2, "c")
qc = QuantumCircuit(a, b, p, c, name="ECDLP_32pts_noise_noqft")
# Put a and b into superposition
qc.h(a)
qc.h(b)
# Oracle call (no-op)
ecdlp_oracle(qc, a, b, p)
qc.barrier()
# Directly measure a and b in the computational basis
qc.measure(a, c[:N_Q])
qc.measure(b, c[N_Q:])
return qc
# IBM Runtime
service = QiskitRuntimeService(channel="ibm_cloud",
token=TOKEN,
instance=INSTANCE)
backend = service.backend(BACKEND)
log.info("Backend → %s", backend.name)
qc_raw = shor_ecdlp_noise_noqft_circuit()
trans = transpile(qc_raw,
backend=backend,
initial_layout=PHYSICAL,
optimization_level=3)
log.info("Circuit depth %d, gate counts %s", trans.depth(), trans.count_ops())
sampler = SamplerV2(mode=backend)
job = sampler.run([trans], shots=SHOTS)
result = job.result()
# Classical post-processing
creg_name = trans.cregs[0].name
counts_raw = result[0].data.__getattribute__(creg_name).get_counts()
def bits_to_int(bs):
return int(bs[::-1], 2)
# Map bitstrings to (a, b) pairs exactly as in the real run
counts = {(bits_to_int(k[N_Q:]), bits_to_int(k[:N_Q])): v
for k, v in counts_raw.items()}
top = sorted(counts.items(), key=lambda kv: kv[1], reverse=True)
# Same invertible-b scan, now interpreted as a pure hardware-noise baseline
top_invertibles = []
for (a_val, b_val), freq in top:
if gcd(b_val, ORDER) != 1:
continue
inv_b = pow(b_val, -1, ORDER)
k_candidate = (-a_val * inv_b) % ORDER
top_invertibles.append(((a_val, b_val), k_candidate, freq))
if len(top_invertibles) == 100:
break
print(
"\nPure hardware-noise baseline (no QFT) — recovered k candidates "
"from top 100 invertible (a, b) pairs:\n"
)
for (a, b), k, count in top_invertibles:
print(f" (a={a:2}, b={b:2}) → k = {k:2} (count = {count})")
# Save raw data
out = {
"experiment": "ECDLP_32pts_Shors_noise_noqft",
"backend": backend.name,
"physical_qubits": PHYSICAL,
"shots": SHOTS,
"counts": counts_raw
}
JSON_PATH = "/Users/steventippeconnic/Documents/QC/Shor_style_ECC_5_Bit_NoQFT_Noise_0.json"
with open(JSON_PATH, "w") as fp:
json.dump(out, fp, indent=4)
log.info("Results saved → %s", JSON_PATH)
# End
///////////////////////////////////////////////////
# Dual QFTs, No Structure (Fully Scrambled Registers)
# Imports
import logging, json
from math import gcd
import numpy as np
from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister, transpile
from qiskit.circuit.library import UnitaryGate, QFT
from qiskit_ibm_runtime import QiskitRuntimeService, SamplerV2
import pandas as pd
# IBMQ
TOKEN = ""
INSTANCE = ""
BACKEND = "ibm_fez"
CAL_CSV = "/Users/steventippeconnic/Downloads/ibm_fez_calibrations_2025-11-22T04_35_16Z.csv"
SHOTS = 16384
# Group parameter (so gcd / inverse logic is identical)
ORDER = 32 # |E(F_p)| = 32
# Logging
logging.basicConfig(level=logging.INFO,
format="%(asctime)s | %(levelname)s | %(message)s")
log = logging.getLogger(__name__)
# Calibration-based qubit pick
def best_qubits(csv_path: str, n: int) -> list[int]:
df = pd.read_csv(csv_path)
df.columns = df.columns.str.strip()
winners = (
df.sort_values(["√x (sx) error", "T1 (us)", "T2 (us)"],
ascending=[True, False, False])
["Qubit"].head(n).tolist()
)
log.info("Best physical qubits: %s", winners)
return winners
N_Q = 5
N_Q_TOTAL = N_Q * 3 # a, b, point
PHYSICAL = best_qubits(CAL_CSV, N_Q_TOTAL)
# Constant-adder modulo 32 as a reusable gate (unused here, kept for continuity)
def add_const_mod32_gate(c: int) -> UnitaryGate:
"""Return a 5-qubit gate that maps |x⟩ ↦ |x+c (mod 32)⟩."""
mat = np.zeros((32, 32))
for x in range(32):
mat[(x + c) % 32, x] = 1
return UnitaryGate(mat, label=f"+{c}")
ADDERS = {c: add_const_mod32_gate(c) for c in range(1, 32)}
def controlled_add(qc: QuantumCircuit, ctrl_qubit, point_reg, constant):
"""Apply |x⟩ → |x+constant (mod 32)⟩ controlled by one qubit."""
qc.append(ADDERS[constant].control(), [ctrl_qubit, *point_reg])
# Noise oracle: same call site, but no operation
def ecdlp_oracle(qc, a_reg, b_reg, point_reg):
# No-op oracle: no a,b→point structure at all.
return
# Fixed 'random' phase masks on a and b to scramble QFT bias
PHASES_A = [0.1732, 0.9410, 1.6180, 2.2740, 2.9670]
PHASES_B = [0.5120, 1.2210, 1.9370, 2.4440, 2.8890]
def apply_phase_scramble(qc: QuantumCircuit, a_reg, b_reg):
"""Apply fixed per-qubit RZ phase masks to a and b before QFT."""
for q, theta in zip(a_reg, PHASES_A):
qc.rz(theta, q)
for q, theta in zip(b_reg, PHASES_B):
qc.rz(theta, q)
# Build the noise circuit WITH QFTs, but no oracle structure on a,b
def shor_ecdlp_noise_qft_scrambled_circuit() -> QuantumCircuit:
a = QuantumRegister(N_Q, "a")
b = QuantumRegister(N_Q, "b")
p = QuantumRegister(N_Q, "p")
c = ClassicalRegister(N_Q * 2, "c")
qc = QuantumCircuit(a, b, p, c, name="ECDLP_32pts_noise_qft_scrambled")
# Put a and b into superposition
qc.h(a)
qc.h(b)
# Phase-scramble a and b so QFT sees a random-looking phase landscape
apply_phase_scramble(qc, a, b)
# Oracle call (no-op, keeps structure slot)
ecdlp_oracle(qc, a, b, p)
qc.barrier()
# QFT on a and b, as in the real algorithm
qc.append(QFT(N_Q, do_swaps=False), a)
qc.append(QFT(N_Q, do_swaps=False), b)
# Measure a and b into classical c
qc.measure(a, c[:N_Q])
qc.measure(b, c[N_Q:])
return qc
# IBM Runtime
service = QiskitRuntimeService(channel="ibm_cloud",
token=TOKEN,
instance=INSTANCE)
backend = service.backend(BACKEND)
log.info("Backend → %s", backend.name)
qc_raw = shor_ecdlp_noise_qft_scrambled_circuit()
trans = transpile(qc_raw,
backend=backend,
initial_layout=PHYSICAL,
optimization_level=3)
log.info("Circuit depth %d, gate counts %s", trans.depth(), trans.count_ops())
sampler = SamplerV2(mode=backend)
job = sampler.run([trans], shots=SHOTS)
result = job.result()
# Classical post-processing
creg_name = trans.cregs[0].name
counts_raw = result[0].data.__getattribute__(creg_name).get_counts()
def bits_to_int(bs):
return int(bs[::-1], 2)
# Map bitstrings to (a, b) pairs exactly as in the real run
counts = {(bits_to_int(k[N_Q:]), bits_to_int(k[:N_Q])): v
for k, v in counts_raw.items()}
top = sorted(counts.items(), key=lambda kv: kv[1], reverse=True)
# Same invertible-b scan, now interpreted as a QFT-scrambled noise baseline
top_invertibles = []
for (a_val, b_val), freq in top:
if gcd(b_val, ORDER) != 1:
continue
inv_b = pow(b_val, -1, ORDER)
k_candidate = (-a_val * inv_b) % ORDER
top_invertibles.append(((a_val, b_val), k_candidate, freq))
if len(top_invertibles) == 100:
break
print(
"\nPhase-scrambled QFT noise baseline — recovered k candidates "
"from top 100 invertible (a, b) pairs:\n"
)
for (a, b), k, count in top_invertibles:
print(f" (a={a:2}, b={b:2}) → k = {k:2} (count = {count})")
# Save raw data
out = {
"experiment": "ECDLP_32pts_Shors_noise_qft_scrambled",
"backend": backend.name,
"physical_qubits": PHYSICAL,
"shots": SHOTS,
"counts": counts_raw
}
JSON_PATH = (
"/Users/steventippeconnic/Documents/QC/"
"Shor_style_ECC_5_Bit_QFT_Scrambled_Noise_0.json"
)
with open(JSON_PATH, "w") as fp:
json.dump(out, fp, indent=4)
log.info("Results saved → %s", JSON_PATH)
# End
//////////////////////////////////////////////////////
# Randomized QFT With Inverted Fourier Partition
# Imports
import logging, json
from math import gcd
import numpy as np
from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister, transpile
from qiskit.circuit.library import UnitaryGate, QFT
from qiskit_ibm_runtime import QiskitRuntimeService, SamplerV2
import pandas as pd
# IBMQ
TOKEN = ""
INSTANCE = ""
BACKEND = "ibm_fez"
CAL_CSV = "/Users/steventippeconnic/Downloads/ibm_fez_calibrations_2025-11-22T05_17_49Z.csv"
SHOTS = 16384
# Group parameter
ORDER = 32
# Logging
logging.basicConfig(level=logging.INFO,
format="%(asctime)s | %(levelname)s | %(message)s")
log = logging.getLogger(__name__)
# Calibration-based qubit pick
def best_qubits(csv_path: str, n: int) -> list[int]:
df = pd.read_csv(csv_path)
df.columns = df.columns.str.strip()
winners = (
df.sort_values(["√x (sx) error", "T1 (us)", "T2 (us)"],
ascending=[True, False, False])
["Qubit"].head(n).tolist()
)
log.info("Best physical qubits: %s", winners)
return winners
N_Q = 5
N_Q_TOTAL = N_Q * 3
PHYSICAL = best_qubits(CAL_CSV, N_Q_TOTAL)
rng = np.random.default_rng(999)
# Build DUAL-QFT noise circuit with random partition
def dual_random_qft_noise_circuit() -> QuantumCircuit:
a = QuantumRegister(N_Q, "a")
b = QuantumRegister(N_Q, "b")
p = QuantumRegister(N_Q, "p")
c = ClassicalRegister(N_Q * 2, "c")
qc = QuantumCircuit(a, b, p, c, name="DualRandomQFT_Noise")
# Unordered global superposition
qc.h(a)
qc.h(b)
# Combine a+b into one 10-qubit pool
ab_qubits = list(a) + list(b)
rng.shuffle(ab_qubits)
# Split into two random halves
half1 = ab_qubits[:5]
half2 = ab_qubits[5:]
log.info(f"Random QFT partitions: half1={half1}, half2={half2}")
# Apply QFT to the first half
qc.append(QFT(len(half1), do_swaps=False), half1)
# Apply another QFT to the second half
qc.append(QFT(len(half2), do_swaps=False), half2)
qc.barrier()
# Measure original a,b layout
qc.measure(a, c[:N_Q])
qc.measure(b, c[N_Q:])
return qc
# IBM Runtime
service = QiskitRuntimeService(
channel="ibm_cloud",
token=TOKEN,
instance=INSTANCE
)
backend = service.backend(BACKEND)
log.info("Backend → %s", backend.name)
qc_raw = dual_random_qft_noise_circuit()
trans = transpile(
qc_raw,
backend=backend,
initial_layout=PHYSICAL,
optimization_level=3
)
log.info("Circuit depth %d, gate counts %s", trans.depth(), trans.count_ops())
sampler = SamplerV2(mode=backend)
job = sampler.run([trans], shots=SHOTS)
result = job.result()
# Post-processing
creg_name = trans.cregs[0].name
counts_raw = result[0].data.__getattribute__(creg_name).get_counts()
def bits_to_int(bs):
return int(bs[::-1], 2)
# Map bitstrings → (a,b)
counts = {(bits_to_int(k[N_Q:]), bits_to_int(k[:N_Q])): v
for k, v in counts_raw.items()}
top = sorted(counts.items(), key=lambda kv: kv[1], reverse=True)
top_invertibles = []
for (a_val, b_val), freq in top:
if gcd(b_val, ORDER) != 1:
continue
inv_b = pow(b_val, -1, ORDER)
k_candidate = (-a_val * inv_b) % ORDER
top_invertibles.append(((a_val, b_val), k_candidate, freq))
if len(top_invertibles) >= 100:
break
print("\nDual-QFT Random Partition Noise — top invertible b-values:\n")
for (a, b), k, count in top_invertibles:
print(f" (a={a:2}, b={b:2}) → k = {k:2} (count = {count})")
# Save raw data
out = {
"experiment": "DualQFT_random_partition_noise",
"backend": backend.name,
"physical_qubits": PHYSICAL,
"shots": SHOTS,
"counts": counts_raw
}
JSON_PATH = (
"/Users/steventippeconnic/Documents/QC/"
"Shor_style_ECC_5_Bit_DualQFT_Random_Noise_0.json"
)
with open(JSON_PATH, "w") as fp:
json.dump(out, fp, indent=4)
log.info("Results saved → %s", JSON_PATH)
# End
//////////////////////////////////////////////////////////////
# Single QFT, No Structure (Fully Scrambled Registers)
# Imports
import logging, json
from math import gcd
import numpy as np
from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister, transpile
from qiskit.circuit.library import UnitaryGate, QFT
from qiskit_ibm_runtime import QiskitRuntimeService, SamplerV2
import pandas as pd
# IBMQ
TOKEN = ""
INSTANCE = ""
BACKEND = "ibm_fez"
CAL_CSV = "/Users/steventippeconnic/Downloads/ibm_fez_calibrations_2025-11-30T21_33_34Z.csv"
SHOTS = 16384
# Group parameter (so gcd / inverse logic is identical)
ORDER = 32 # |E(F_p)| = 32
# Logging
logging.basicConfig(level=logging.INFO,
format="%(asctime)s | %(levelname)s | %(message)s")
log = logging.getLogger(__name__)
# Calibration-based qubit pick
def best_qubits(csv_path: str, n: int) -> list[int]:
df = pd.read_csv(csv_path)
df.columns = df.columns.str.strip()
winners = (
df.sort_values(["√x (sx) error", "T1 (us)", "T2 (us)"],
ascending=[True, False, False])
["Qubit"].head(n).tolist()
)
log.info("Best physical qubits: %s", winners)
return winners
N_Q = 5
N_Q_TOTAL = N_Q * 3 # a, b, point
PHYSICAL = best_qubits(CAL_CSV, N_Q_TOTAL)
# Constant-adder modulo 32 as a reusable gate (unused here, kept for continuity)
def add_const_mod32_gate(c: int) -> UnitaryGate:
"""Return a 5-qubit gate that maps |x⟩ ↦ |x+c (mod 32)⟩."""
mat = np.zeros((32, 32))
for x in range(32):
mat[(x + c) % 32, x] = 1
return UnitaryGate(mat, label=f"+{c}")
ADDERS = {c: add_const_mod32_gate(c) for c in range(1, 32)}
def controlled_add(qc: QuantumCircuit, ctrl_qubit, point_reg, constant):
"""Apply |x⟩ → |x+constant (mod 32)⟩ controlled by one qubit."""
qc.append(ADDERS[constant].control(), [ctrl_qubit, *point_reg])
# Noise oracle: same call site, but no operation
def ecdlp_oracle(qc, a_reg, b_reg, point_reg):
# No-op oracle: no a,b→point structure at all.
return
# Fixed "random" phase masks on a and b to scramble QFT bias
PHASES_A = [0.1732, 0.9410, 1.6180, 2.2740, 2.9670]
PHASES_B = [0.5120, 1.2210, 1.9370, 2.4440, 2.8890]
def apply_phase_scramble(qc: QuantumCircuit, a_reg, b_reg):
"""Apply fixed per-qubit RZ phase masks to a and b before QFT."""
for q, theta in zip(a_reg, PHASES_A):
qc.rz(theta, q)
for q, theta in zip(b_reg, PHASES_B):
qc.rz(theta, q)
# Build the noise circuit with ONE global QFT on a∪b, no oracle structure on a,b
def shor_ecdlp_noise_qft_scrambled_circuit() -> QuantumCircuit:
a = QuantumRegister(N_Q, "a")
b = QuantumRegister(N_Q, "b")
p = QuantumRegister(N_Q, "p")
c = ClassicalRegister(N_Q * 2, "c")
qc = QuantumCircuit(a, b, p, c, name="ECDLP_32pts_noise_qft_scrambled_1QFT")
# Put a and b into superposition
qc.h(a)
qc.h(b)
# Phase-scramble a and b so QFT sees a random-looking phase landscape
apply_phase_scramble(qc, a, b)
# Oracle call (no-op, keeps structure slot)
ecdlp_oracle(qc, a, b, p)
qc.barrier()
# Single global QFT on all a∪b qubits (10-qubit QFT)
ab_qubits = list(a) + list(b)
qc.append(QFT(len(ab_qubits), do_swaps=False), ab_qubits)
# Measure a and b into classical c
qc.measure(a, c[:N_Q])
qc.measure(b, c[N_Q:])
return qc
# IBM Runtime
service = QiskitRuntimeService(channel="ibm_cloud",
token=TOKEN,
instance=INSTANCE)
backend = service.backend(BACKEND)
log.info("Backend → %s", backend.name)
qc_raw = shor_ecdlp_noise_qft_scrambled_circuit()
trans = transpile(qc_raw,
backend=backend,
initial_layout=PHYSICAL,
optimization_level=3)
log.info("Circuit depth %d, gate counts %s", trans.depth(), trans.count_ops())
sampler = SamplerV2(mode=backend)
job = sampler.run([trans], shots=SHOTS)
result = job.result()
# Classical post-processing
creg_name = trans.cregs[0].name
counts_raw = result[0].data.__getattribute__(creg_name).get_counts()
def bits_to_int(bs):
return int(bs[::-1], 2)
# Map bitstrings to (a, b) pairs exactly as in the real run
counts = {(bits_to_int(k[N_Q:]), bits_to_int(k[:N_Q])): v
for k, v in counts_raw.items()}
top = sorted(counts.items(), key=lambda kv: kv[1], reverse=True)
# Same invertible-b scan, now interpreted as a single-QFT scrambled noise baseline
top_invertibles = []
for (a_val, b_val), freq in top:
if gcd(b_val, ORDER) != 1:
continue
inv_b = pow(b_val, -1, ORDER)
k_candidate = (-a_val * inv_b) % ORDER
top_invertibles.append(((a_val, b_val), k_candidate, freq))
if len(top_invertibles) == 100:
break
print("\nPhase-scrambled single-QFT noise baseline — "
"recovered k candidates from top 100 invertible (a, b) pairs:\n")
for (a, b), k, count in top_invertibles:
print(f" (a={a:2}, b={b:2}) → k = {k:2} (count = {count})")
# Save raw data
out = {
"experiment": "ECDLP_32pts_Shors_noise_qft_scrambled_1QFT",
"backend": backend.name,
"physical_qubits": PHYSICAL,
"shots": SHOTS,
"counts": counts_raw
}
JSON_PATH = (
"/Users/steventippeconnic/Documents/QC/"
"Shor_style_ECC_5_Bit_QFT_Scrambled_1QFT_Noise_0.json"
)
with open(JSON_PATH, "w") as fp:
json.dump(out, fp, indent=4)
log.info("Results saved → %s", JSON_PATH)
# End
/////////////////////////////////////////////////////////////
# Randomized Single QFT With Inverted Fourier Partition
# Imports
import logging, json
from math import gcd
import numpy as np
from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister, transpile
from qiskit.circuit.library import UnitaryGate, QFT
from qiskit_ibm_runtime import QiskitRuntimeService, SamplerV2
import pandas as pd
# IBMQ
TOKEN = ""
INSTANCE = ""
BACKEND = "ibm_fez"
CAL_CSV = "/Users/steventippeconnic/Downloads/ibm_fez_calibrations_2025-11-30T21_33_34Z.csv"
SHOTS = 16384
# Group parameter
ORDER = 32
# Logging
logging.basicConfig(level=logging.INFO,
format="%(asctime)s | %(levelname)s | %(message)s")
log = logging.getLogger(__name__)
# Calibration-based qubit pick
def best_qubits(csv_path: str, n: int) -> list[int]:
df = pd.read_csv(csv_path)
df.columns = df.columns.str.strip()
winners = (
df.sort_values(["√x (sx) error", "T1 (us)", "T2 (us)"],
ascending=[True, False, False])
["Qubit"].head(n).tolist()
)
log.info("Best physical qubits: %s", winners)
return winners
N_Q = 5
N_Q_TOTAL = N_Q * 3
PHYSICAL = best_qubits(CAL_CSV, N_Q_TOTAL)
rng = np.random.default_rng(999)
# Build SINGLE-QFT noise circuit with random partition
def dual_random_qft_noise_circuit() -> QuantumCircuit:
a = QuantumRegister(N_Q, "a")
b = QuantumRegister(N_Q, "b")
p = QuantumRegister(N_Q, "p")
c = ClassicalRegister(N_Q * 2, "c")
qc = QuantumCircuit(a, b, p, c, name="DualRandomQFT_Noise")
# Unordered global superposition
qc.h(a)
qc.h(b)
# Combine a+b into one 10-qubit pool
ab_qubits = list(a) + list(b)
rng.shuffle(ab_qubits)
# Split into two random halves
half1 = ab_qubits[:5]
half2 = ab_qubits[5:]
log.info(f"Random QFT partitions: half1={half1}, half2={half2}")
# Apply QFT to ONLY the first half (single QFT variant)
qc.append(QFT(len(half1), do_swaps=False), half1)
qc.barrier()
# Measure original a,b layout
qc.measure(a, c[:N_Q])
qc.measure(b, c[N_Q:])
return qc
# IBM Runtime
service = QiskitRuntimeService(
channel="ibm_cloud",
token=TOKEN,
instance=INSTANCE
)
backend = service.backend(BACKEND)
log.info("Backend → %s", backend.name)
qc_raw = dual_random_qft_noise_circuit()
trans = transpile(
qc_raw,
backend=backend,
initial_layout=PHYSICAL,
optimization_level=3
)
log.info("Circuit depth %d, gate counts %s", trans.depth(), trans.count_ops())
sampler = SamplerV2(mode=backend)
job = sampler.run([trans], shots=SHOTS)
result = job.result()
# Post-processing
creg_name = trans.cregs[0].name
counts_raw = result[0].data.__getattribute__(creg_name).get_counts()
def bits_to_int(bs):
return int(bs[::-1], 2)
# Map bitstrings → (a,b)
counts = {(bits_to_int(k[N_Q:]), bits_to_int(k[:N_Q])): v
for k, v in counts_raw.items()}
top = sorted(counts.items(), key=lambda kv: kv[1], reverse=True)
top_invertibles = []
for (a_val, b_val), freq in top:
if gcd(b_val, ORDER) != 1:
continue
inv_b = pow(b_val, -1, ORDER)
k_candidate = (-a_val * inv_b) % ORDER
top_invertibles.append(((a_val, b_val), k_candidate, freq))
if len(top_invertibles) >= 100:
break
print("\nDual-QFT Random Partition Noise — top invertible b-values:\n")
for (a, b), k, count in top_invertibles:
print(f" (a={a:2}, b={b:2}) → k = {k:2} (count = {count})")
# Save raw data
out = {
"experiment": "DualQFT_random_partition_noise",
"backend": backend.name,
"physical_qubits": PHYSICAL,
"shots": SHOTS,
"counts": counts_raw
}
JSON_PATH = (
"/Users/steventippeconnic/Documents/QC/"
"Shor_style_ECC_5_Bit_Key_Noise_Baseline_"
"Scramble_IF_Single_QFT_0.json"
)
with open(JSON_PATH, "w") as fp:
json.dump(out, fp, indent=4)
log.info("Results saved → %s", JSON_PATH)
# End
/////////////////////////////////////////////////////////////
# Real Oracle and single 10-Qubit QFT
# Imports
import logging, json
from math import gcd
import numpy as np
from qiskit import QuantumCircuit, QuantumRegister, ClassicalRegister, transpile
from qiskit.circuit.library import UnitaryGate, QFT
from qiskit_ibm_runtime import QiskitRuntimeService, SamplerV2
import pandas as pd
# IBMQ
TOKEN = ""
INSTANCE = ""
BACKEND = "ibm_fez"
CAL_CSV = "/Users/steventippeconnic/Downloads/ibm_fez_calibrations_2025-11-30T23_33_22Z.csv"
SHOTS = 16384
# Toy-curve parameters (order-32 subgroup of E(F_p))
ORDER = 32 # |E(F_p)| = 32
P_IDX = 1 # Generator P -> index 1
Q_IDX = 23 # Public point Q = kP, here “23 mod 32” for k = 7
# Logging helper
logging.basicConfig(level=logging.INFO,
format="%(asctime)s | %(levelname)s | %(message)s")
log = logging.getLogger(__name__)
# Calibration-based qubit pick
def best_qubits(csv_path: str, n: int) -> list[int]:
df = pd.read_csv(csv_path)
df.columns = df.columns.str.strip()
winners = (
df.sort_values(["√x (sx) error", "T1 (us)", "T2 (us)"],
ascending=[True, False, False])
["Qubit"].head(n).tolist()
)
log.info("Best physical qubits: %s", winners)
return winners
N_Q = 5
N_Q_TOTAL = N_Q * 3 # a, b, point
PHYSICAL = best_qubits(CAL_CSV, N_Q_TOTAL)
# Constant-adder modulo 32 as a reusable gate
def add_const_mod32_gate(c: int) -> UnitaryGate:
"""Return a 5-qubit gate that maps |x⟩ ↦ |x+c (mod 32)⟩."""
mat = np.zeros((32, 32))
for x in range(32):
mat[(x + c) % 32, x] = 1
return UnitaryGate(mat, label=f"+{c}")
ADDERS = {c: add_const_mod32_gate(c) for c in range(1, 32)}
def controlled_add(qc: QuantumCircuit, ctrl_qubit, point_reg, constant):
"""Apply |x⟩ → |x+constant (mod 32)⟩ controlled by one qubit."""
qc.append(ADDERS[constant].control(), [ctrl_qubit, *point_reg])
# Oracle U_f : |a⟩|b⟩|0⟩ ⟶ |a⟩|b⟩|aP + bQ⟩ (index arithmetic mod 32)
def ecdlp_oracle(qc, a_reg, b_reg, point_reg):
# a * P contribution
for i in range(N_Q):
constant = (P_IDX * (1 << i)) % ORDER
if constant:
controlled_add(qc, a_reg[i], point_reg, constant)
# b * Q contribution
for i in range(N_Q):
constant = (Q_IDX * (1 << i)) % ORDER
if constant:
controlled_add(qc, b_reg[i], point_reg, constant)
# Build the Shor circuit variant with a single 10-qubit QFT on a∪b
def shor_ecdlp_single_qft_circuit() -> QuantumCircuit:
a = QuantumRegister(N_Q, "a")
b = QuantumRegister(N_Q, "b")
p = QuantumRegister(N_Q, "p")
c = ClassicalRegister(N_Q * 2, "c")
qc = QuantumCircuit(a, b, p, c, name="ECDLP_32pts_singleQFT")
# Same uniform superposition on a,b
qc.h(a)
qc.h(b)
# Same real aP + bQ oracle
ecdlp_oracle(qc, a, b, p)
qc.barrier()
# Single 10-qubit QFT across a ∪ b instead of two 5-qubit QFTs
ab_qubits = list(a) + list(b)
qc.append(QFT(len(ab_qubits), do_swaps=False), ab_qubits)
# Measure a and b into classical bits
qc.measure(a, c[:N_Q])
qc.measure(b, c[N_Q:])
return qc
# IBM Runtime execution
service = QiskitRuntimeService(channel="ibm_cloud",
token=TOKEN,
instance=INSTANCE)
backend = service.backend(BACKEND)
log.info("Backend → %s", backend.name)
qc_raw = shor_ecdlp_single_qft_circuit()
trans = transpile(qc_raw,
backend=backend,
initial_layout=PHYSICAL,
optimization_level=3)
log.info("Circuit depth %d, gate counts %s", trans.depth(), trans.count_ops())
sampler = SamplerV2(mode=backend)
job = sampler.run([trans], shots=SHOTS)
result = job.result()
# Classical post-processing
creg_name = trans.cregs[0].name
counts_raw = result[0].data.__getattribute__(creg_name).get_counts()
def bits_to_int(bs):
return int(bs[::-1], 2)
# Map measurement bitstrings into (a, b) grid exactly as in the paper
counts = {(bits_to_int(k[N_Q:]), bits_to_int(k[:N_Q])): v
for k, v in counts_raw.items()}
top = sorted(counts.items(), key=lambda kv: kv[1], reverse=True)
print("\nSingle-QFT real-oracle run — top 100 (a, b) bins:\n")
for i, ((a_val, b_val), freq) in enumerate(top[:100], start=1):
print(f"{i:3d}: (a={a_val:2}, b={b_val:2}) count = {freq}")
# Save raw data for Three.js / heatmaps
out = {
"experiment": "ECDLP_32pts_Shors_singleQFT",
"backend": backend.name,
"physical_qubits": PHYSICAL,
"shots": SHOTS,
"P_IDX": P_IDX,
"Q_IDX": Q_IDX,
"ORDER": ORDER,
"counts": counts_raw
}
JSON_PATH = (
"/Users/steventippeconnic/Documents/QC/"
"Shors_ECC_5_Bit_SingleQFT_RealOracle_0.json"
)
with open(JSON_PATH, "w") as fp:
json.dump(out, fp, indent=4)
log.info("Results saved → %s", JSON_PATH)
# End
/////////////////////////////////////////////////////////////
// code for all Threejs visuals
// Config
const HALF_BITS = 5; // 5 per axis
const TOTAL_BITS = 2 * HALF_BITS; // 10
const GRID = 1 << HALF_BITS; // 32
const MOD = GRID; // 32
// Load JSON (replace for experiment run)
async function loadQuantumData() {
const res = await fetch('Your_experiment_results.json');
const data = await res.json();
return data.counts;
}
// Three.js setup
const scene = new THREE.Scene();
const camera = new THREE.PerspectiveCamera(
75, window.innerWidth / window.innerHeight, 0.1, 1000
);
const renderer = new THREE.WebGLRenderer({ antialias: true });
renderer.setSize(window.innerWidth, window.innerHeight);
document.body.appendChild(renderer.domElement);
// Controls & lighting
const controls = new THREE.OrbitControls(camera, renderer.domElement);
const light = new THREE.DirectionalLight(0xffffff, 1);
light.position.set(10, 10, 10);
scene.add(light);
// Camera
camera.position.set(0, 30, 60);
camera.lookAt(0, 0, 0);
// Globals
let mesh;
let redDots = [];
let time = 0;
// Helpers
const pad10 = s => s.padStart(TOTAL_BITS, '0').slice(-TOTAL_BITS);
const rev = s => s.split('').reverse().join('');
// Parse into classical (a,b) and use those as display (u,v)
function parseEntries(counts) {
const entries = [];
for (const [bit, cRaw] of Object.entries(counts)) {
const b10 = pad10(bit);
const left = b10.slice(0, HALF_BITS); // raw left 5
const right = b10.slice(HALF_BITS); // raw right 5
const a = parseInt(rev(right), 2); // a = int(right[::-1], 2)
const b = parseInt(rev(left), 2); // b = int(left[::-1], 2)
const u = a;
const v = b;
entries.push({ bit, a, b, u, v, count: Number(cRaw) });
}
return entries;
}
function buildMatrix(entries) {
const matrix = Array.from({ length: GRID }, () => Array(GRID).fill(0));
let maxCount = 0;
for (const e of entries) {
matrix[e.u][e.v] = e.count;
if (e.count > maxCount) maxCount = e.count;
}
return { matrix, maxCount };
}
// Build surface + dots
function createWaveSurface(matrix, maxCount) {
const WIDTH = GRID * 2;
const SEGMENTS = WIDTH;
const STEP = WIDTH / (GRID - 1);
const geometry = new THREE.PlaneGeometry(WIDTH, WIDTH, SEGMENTS, SEGMENTS);
const colors = [];
const gridX = SEGMENTS + 1;
const gridY = SEGMENTS + 1;
for (let y = 0; y < gridY; y++) {
for (let x = 0; x < gridX; x++) {
const color = new THREE.Color(0x00ff00); // uniform green mesh
colors.push(color.r, color.g, color.b);
}
}
geometry.setAttribute('color', new THREE.Float32BufferAttribute(colors, 3));
const material = new THREE.MeshBasicMaterial({ vertexColors: true, wireframe: true });
mesh = new THREE.Mesh(geometry, material);
mesh.rotation.x = -Math.PI / 2;
mesh.userData = { matrix, maxCount, GRID, STEP };
scene.add(mesh);
// Red dots at every (u,v)
const dotMat = new THREE.MeshBasicMaterial({ color: 0xff0000 });
for (let v = 0; v < GRID; v++) {
for (let u = 0; u < GRID; u++) {
const dot = new THREE.Mesh(new THREE.SphereGeometry(0.15, 8, 8), dotMat);
dot.position.set(
(u - (GRID - 1) / 2) * STEP,
0,
(v - (GRID - 1) / 2) * STEP
);
redDots.push(dot);
scene.add(dot);
}
}
}
// Animate
function animate() {
requestAnimationFrame(animate);
time += 0.2;
if (!mesh) {
renderer.render(scene, camera);
return;
}
const { matrix, maxCount, GRID } = mesh.userData;
const pos = mesh.geometry.attributes.position;
const gridX = mesh.geometry.parameters.widthSegments + 1;
const gridY = mesh.geometry.parameters.heightSegments + 1;
for (let i = 0; i < pos.count; i++) {
const x = i % gridX;
const y = Math.floor(i / gridX);
const u = Math.floor(x / (gridX / GRID));
const v = Math.floor(y / (gridY / GRID));
const amp = matrix[u]?.[v] ? matrix[u][v] / maxCount : 0;
const wave = Math.sin((x + time) * 0.4) * Math.cos((y + time) * 0.4);
pos.setZ(i, amp * wave * 20);
}
// Move dots with amplitude
redDots.forEach((dot, idx) => {
const u = idx % GRID;
const v = Math.floor(idx / GRID);
const amp = matrix[u]?.[v] ? matrix[u][v] / maxCount : 0;
dot.position.y = amp * 20 + 0.5;
});
pos.needsUpdate = true;
controls.update();
renderer.render(scene, camera);
}
// Main
loadQuantumData().then(counts => {
const entries = parseEntries(counts);
const { matrix, maxCount } = buildMatrix(entries);
createWaveSurface(matrix, maxCount);
animate();
});